ヘリウム・希ガス吸着膜のナノ摩擦

研究の背景

原子間力顕微鏡を始めとする実験技術の進歩によってミクロスケールでの摩擦の測定が可能となり，ナノトライボロジーと呼ばれる研究分野が登場した[1]． その中で物理吸着膜の滑り摩擦は，界面摩擦のメカニズムにミクロな視点からアプローチができるとして，実験的にも理論的にも興味がもたれている．

これまでに，Krim等により水晶マイクロバランス(QCM)法が開発され，金属基板上の希ガス吸着膜等の滑り摩擦の測定が行われた．彼女らは， Au基板上のKr単層膜(Kr/Au)の滑り摩擦が基板に対して不整合な固相吸着膜では液相膜に比べて小さくなると報告している[2]．一方，2002年にはMisturaらは同じくKr/Auの滑り摩擦を測定し，外力を緩やかに上昇させると摩擦力の急激な減少が起きることを見いだし『ピン止め-滑り(pinning-depinning)』の動的転移であると主張している[3]． このように物理吸着膜の単層膜の滑り摩擦は興味深い現象が観測されている状況であった．しかしながら金属基板上の吸着膜の摩擦力は大きく，精密な測定が困難であった．特に，理論的に明らかでない多層膜の滑り摩擦の振る舞い，モデル計算のみ行われている動的転移の緩和現象[4]の解明は実験的に大きな課題であった．

以上の背景から，分子間力が弱く滑り摩擦が小さいことが期待されるHe吸着膜と典型的な吸着基板であるグラファイト基板を用いてグラファイト基板上のHe吸着膜の滑り摩擦の研究が開始された．

研究の特色・研究成果

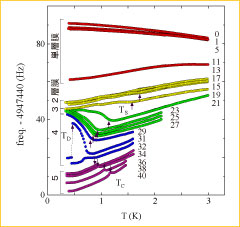図1. 基板振幅0.4nmにおける^4He吸着膜の面密度毎の共振周波数の温度変化．吸着膜の各層は異なる曲線の色で示す．図中の矢印は，温度減少に伴い滑り摩擦が減少を開始する温度T_S, 増加する温度T_D, 及び超流動転移温度T_C.

本研究では滑り摩擦を，研究室独自に開発したグラファイト基板を用いた水晶マイクロバランス(QCM)法により測定した． さらに基板として比表面積が大きなグラフォイル(20m^2/g)を使用し，質量の小さいHe原子でも高精度な滑り摩擦の測定を可能にした． 測定はHe吸着膜の面密度毎に摩擦力の温度依存性，基板振幅依存性等を系統的に行った．

図1に，測定で得られた基板振幅0.4nmにおける５原子層までの^4He吸着膜の面密度毎の共振周波数の温度変化を示す． 滑り摩擦が十分に大きければ膜の面密度に比例し周波数は低下する． 一方，摩擦力が小さく吸着膜が滑る場合には，周波数の低下は抑制される． 図から明らかなように，He吸着膜の滑り摩擦は興味深い振る舞いを示す． 単層膜では滑り摩擦が非常に小さく，また多層膜においてもかなり小さいことが明らかとなった． これはHe原子の分子間力が弱いことに因ると考えられる． 特に，２層膜では2K程度，３層膜では1K程度のT_S以下の低温から滑り摩擦がさらに減少する． ４層膜ではHe吸着膜の超流動により，T_Dより突然に滑り摩擦が増加する面白い現象が見出された． このように多彩な振る舞いが本研究により初めて明らかにされた[4,5]．

結果1. 多層膜の滑り摩擦

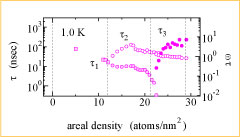図2. 温度1.0K，基板振幅0.4nmにおける^4He吸着膜の層毎のスリップ時間の面密度変化． 図中の点線は吸着膜の各原子層の開始を表す． 灰色の記号がτ_1，白抜きがτ_2，黒塗りがτ_3を示す．

上述した測定から明らかなように，He吸着膜の滑り摩擦は膜の明確な層構造を反映して変化する． そこで我々の研究室では，吸着膜の各層間が互いに滑るモデルに基づき解析を行った．

図2に温度1Kにおける層間毎のスリップ時間τの面密度変化を示す． ここでスリップ時間とは摩擦により膜の運動量が1/eに減衰するまでの時間であり，摩擦力の逆数に比例する． 図のように２層膜では基板と第１原子層間のスリップ時間τ_1は，第１原子層と第２原子層間のスリップ時間τ_2より１桁程度小さい． これは，基板と第１原子層間の摩擦力は大きく，第１原子層と第２原子層間では小さいことを意味する． さらに，２層膜におけるスリップ時間の温度依存性を解析し，上述のT_S以下の低温では第１原子層と第２原子層間の滑り摩擦がさらに減少 することを明らかにした．

結果2. 滑り摩擦の準安定性とその緩和

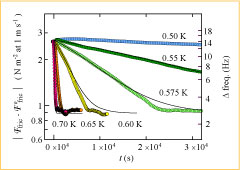図3. 基板振幅1.0nm, 0.6nmから0.2nmへの振幅の降下後の基板振幅0.2nmにおける摩擦力の時間変化． ^4He吸着膜の面密度23atoms/nm^2(３原子膜)． 滑り摩擦の変化は対数軸を用い，対応する共振周波数の変化は右軸に示した． 各実線はモデルによる数値計算の結果．

結果1で述べたように２層膜，３層膜ではT_S以下の低温で摩擦力は減少し，さらに基板振幅（吸着膜に働く外力に対応する）が大きいほど減少が大きいことが測定により明らかとなった． 滑り摩擦の振幅依存性から，振幅の切り替えに対して滑り摩擦の緩和が観測されることが期待される． 図3. は，３層膜の基板振幅1.0から0.2nmへの降下後の滑り摩擦の時間変化である． 滑り摩擦はある値に達するまで対数プロットで直線的に変化する．また緩和時間は温度に強く依存する． ここでは図を示していないが，振幅の上昇後の滑り摩擦の時間変化は時間に対して対数関数的であり，また温度依存性も強くない．

これら緩和現象を理解するために振動基板上の吸着膜の滑り摩擦の新しいモデルを提案した． このモデルでは，振動基板上では吸着膜の一部の領域で原子の再配列がポテンシャル障壁を越えて起こり，低摩擦ドメインを生じると考える． このドメインの生成・消滅のポテンシャル障壁が振幅に依存すると仮定すれば，振幅降下と上昇の両者の緩和現象を測定結果の温度依存を含めて再現する．

以上，我々の研究室ではグラファイト基板上の4He吸着膜の滑り摩擦をはじめて測定し，多彩な滑り摩擦の現象を見出した． 特に多層膜の滑り摩擦>や滑り摩擦の準安定性とその緩和で得られた吸着膜の滑り摩擦のミクロな描像は，本研究によりはじめて示されたものでり，界面摩擦のメカニズムにミクロな視点から重要な知見を与えたと考えている．